The following information is for the EMANT380
Measure Strain
Learn:
- Strain Measurement
A typical quarter bridge strain measurement solution comprises
- the EMANT380 Bluetooth DAQ (or EMANT300 USB DAQ). Power supply for the EMANT380 not shown.
- Bridge Sensor Application Adaptor
- Bridge Completion Network
- Mounted Strain Gauge
When an object is stretched due to an external force and the length of the object increases from L to L+ΔL, the ratio ΔL/L is called strain.
ε = ΔL/L
As the ratio of deformation is often very small, it is often represented in a units of 10-6 or μstrain
A strain gauge (gage) can be used to measure the strain of this object. The most common type of strain gauge (gage) consists of a flexible backing which supports a metallic foil pattern etched onto the backing. As the object is deformed, the foil pattern is deformed, causing its electrical resistance to change. This resistance change, usually measured using a Wheatstone bridge circuit, can be used to calculate the exact amount of deformation by means of the quantity known as the gauge (gage) factor.
The gauge(gage) factor of a strain gauge (gage) relates strain to change in electrical resistance. The gauge (gage) factor GF is defined by the formula
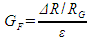
where RG is the resistance of the undeformed gauge, ΔR is the change in resistance caused by strain, and ε is strain.
In our example, we will use one strain gauge (gage) with GF=2, RG = 120 ohms and connected in a quarter bridge configuration. The bridge is excited at VEXC=3.3V.
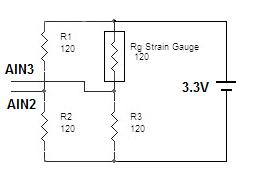
The voltage output of the wheatstone bridge VO (seen at the differential input AIN3, AIN2) is given by
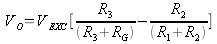
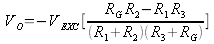
If the bridge is balanced VO =0 since all the resistances are equal. When a strain is applied, RG becomes R + ΔR and substituting R to all the other resistances, the equation becomes
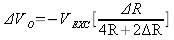
If we assume 2 ΔR << 4R
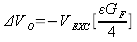
Finally substituting VEXC=3.3V, GF=2, we obtain (in ustrains)
ε = -ΔVO * 1000000 / 1.66